Defining Object Convexity
This feature measures how complex or concave an object’s shape is.
Convexity is how an object’s shape deviates from a simple, smooth, and convex outline.
The Importance of Object Convexity
Understanding the convexity of objects is crucial for accurate segmentation.
Objects with higher convexity values have more intricate and irregular shapes, with curved or concave regions.
These complex shapes can pose challenges for segmentation algorithms, as accurately delineating the boundaries of such objects requires advanced techniques. We will discuss how convexity impacts model design in Lesson 5.4.
Calculating Object Convexity
The convexity measure is calculated by comparing the perimeter of an object’s actual shape (contour) with the perimeter of its simplest convex shape (convex hull).
The convex hull is the smallest convex polygon that fully encloses the object.
The convexity measure is determined by the difference between these two perimeters, normalized by the object’s perimeter. Higher values indicate objects with more complex shapes and greater deviations from a simple convex outline.
The convexity measures are then aggregated and visualized using a graph showing the distribution of convexity values for objects in both the training and validation sets.
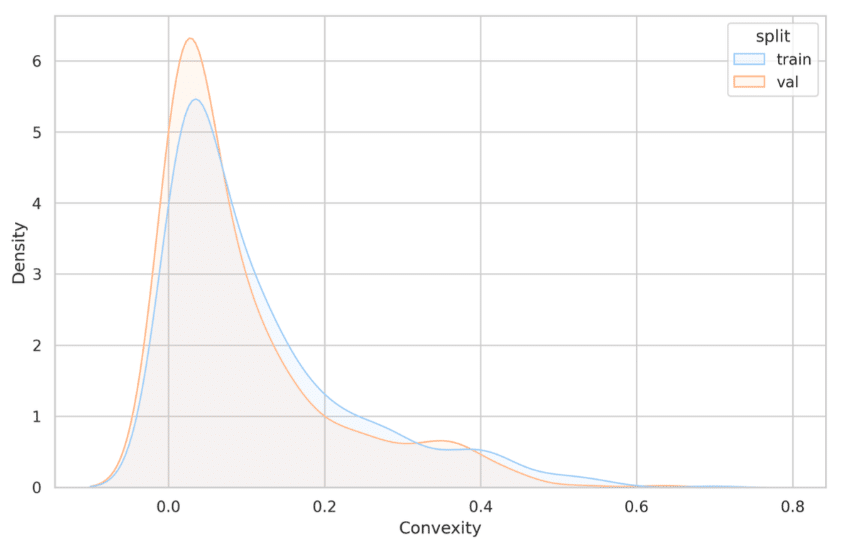
Here’s how Object Convexity is calculated in DataGradients.
Exploring Object Convexity Through Examples
To further understand object convesity, let’s turn our attention to three examples.
Example 1: Near Full Convexity

This object is not fully convex, but almost. It will be easier for the segmentation model to predict.
Example 2: Lack of Convexity at the Edges

The main object here still has an overall convex shape, but the edges are not convex at all. While the core of the object may be easy to predict, the model may struggle to properly predict the edges.
Example 3: Concave Object

Here we have an object whose overall shape is concave. This time, even the core of the object may be challenging for the model to predict because of how narrow it is.
How object convexity impacts model design
When your dataset exhibits high object convexity values, signifying smooth, simple, and compact shapes, you can implement two practical strategies.
Firstly, opt for models with less complex decoders. With simple shapes, elaborate decoders aren’t usually required; basic ones can adequately recreate the original shapes.
Secondly, consider lower resolution during inferencing. With high convexity objects, reducing the resolution will lead to minor information loss, while boosting the speed of your model.
However, if your dataset shows low object convexity values, representing intricate shapes, your approach should differ. Here, you’ll need models with more complex decoders to handle these nuanced shapes. Furthermore, higher resolution during inferencing may be necessary to accurately capture the details. We expand on this in Lesson 5.4.
